Инженерлік мүсін. Компьютерлік графика. Безье қисық сызығы

1955-75 жылы шыққан Citroёn DS автомобилін қараңызшы темір мен шыныдан жасалған нағыз мүсін. Автомобилінің кузовының бетінің доға тәріздес иіліп, бетіндегі әр сызық түйісіп көлемді көріністі құрайды. Орнында тұрғанын өзінде алға ұмтылып ұшып бара жатқандай әсер береді.

Сурет-1. Citroёn DS
1950 жылдардың басында АҚШ-тың Массачусетс технологиялық институтында CNC -компьютерлік сандық командамен басқарылатын станок ойланып табылды. Келесідей мәселелер өз шешімін күтті:
— детальдің цифрлы моделін алу жолын қарастыру;
— детальдің цифрлық моделі бойынша өңдеп шығаратын станокты басқаратын программаны жасау.
Жоғарыда әңгіме етілген Citroёn DS автомобилінің кузовы «инженерлік мүсін»-ді дәл жасап шығару үшін оны математикалық аппаратпен сипаттауды қажет етті. Автокөлік жасау, аэрокосмос салаларының тапсырыстары бойынша әртүрлі зерттеу топтары үш кеңістегі модельдеу мүмкіншілігін зерттеуге кірісті.
1959 жылы Citroёn автокөлік жасау компаниясына жұмыс істеген француз математигі Поль де Кастельжо «бақылаушы нүктелер» көмегімен геометриялық қасиеттерін сипаттау арқылы «тегіс беттерді» алу жолын ұсынды. Бірақ та ол ашқан сызықтар басқа француз Безье атымен аталады. Поль де Кастельжо жаңалығы «өндірістік құпия болып» сақталынды.
1962 жылдары «Рено» автокөлік компаниясының инженері Безье Пьер көпшілікке өз жаңалығын ұсынды (Поль де Кастельжодан дербес дәл сондай жаңалық жасады). Көп уақыт UNISURF автокөлік кузовтарын жобалайтын компьютерлік бағдарламаны жасаумен шұғылданды. Аталған компьютерлік программаны жасау барысында өнертабыс жасап компьютерлік графиканы дамытуға өз үлесін қосты.
Қазір 3D жобалау арқылы заттың моделін алу заманға ілтипат білдіру болып кетті. Ондай ілтипатты бізде көрсетейік. 3D принтер.

Сурет-2. «3D принтер». Барабандағы пластик шыбықты балқыту арқылы төмендегі мүсінді құйып шықты. Мүсін дәл ортада платформа үстінде тұр («мүйізге» ұқсас).
3D принтер көмегімен алынған мүсін іші қуыс. Қабырғасының қалыңдығы 2 мм. Мүсінді 3D принтер табанынан бастап үстіне дейін бір қабат пластмасса үстіне екінші қабат пластмассаны түзеу арқылы жасап шығарды. Әр қабаттың қалыңдығы мөлшермен 0,3 мм және өзіне тән профилі бар. Профильді түзеу үшін платформа принтердің басының астында қозғалады. Платформаны қозғау үшін екі қозғалтқыш қолданылады. Әр қозғалтқыш платформаны ілгері — кері қозғалысқа келтіреді, яғни х, у бағыттары бойынша.
Енді ең басты. Қалайша қарапайым ілгері – кері қозғалыс арқылы мүсінді құрайтын жаңа қабаттың профилін алуға болатын ойланайық. Көмекке математика келеді. Профиль қисық сызықтар контурынан тұрады. Егер қисық сызықты құрайтын барлық нүктелердің координаталарын білсек онда нүктелерді х, у координатасын анықтап платформа қозғалтқыштарына бере берсек болғаны. Алайда бәрі оңай болса ғой. Профиль контурын анықтайтын графиктің функциясын табу қиын. Пьер Безье қалаған контурын алу үшін функцияны тауып алды. Оның көмегімен координата жазығында оп-оңай конструктор қалаған пішімде кез-келген сызық түсіре алды.
Шын мәнінде 3D принтеріміз CNC станогы ғой!
Базье неге қол жеткізгенін түсіну үшін «Безьенің» екінші дәрежелі қисық сызығын қарастырайық.
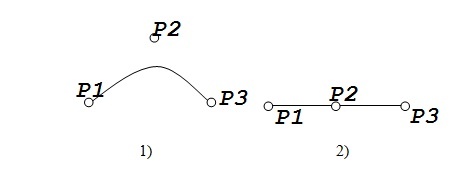
Сурет -3. Екінші дәрежелі Безье сызықтары. Бірінші қисық сызық салыну үшін тең бүйірлі үшбұрыштың төбелерінде жататын үш нүкте таңдалынып алынады. Екінші қисық сызық салыну үшін бір түзу бойында, бір-бірінен бірдей қашықтықта жататын үш нүкте алынады.
Екінші дәрежелі Безье сызығының қасиетін бағалау үшін доғаның «алу» жолын көз алдымызға елестетіп көрейік. 3-ші суреттегі ортаңғы нүкте төмен сырғып түскенде «доға» түзуге айналғанын елестету қиын емес. Мұндай қасиеті бар «қисық» сызықты қалай сызуға болады?
Теорияда екінші дәрежелі Безье қисық сызығының теңдеуі келесідей:
B(T) = (1-t)^2 * P0 + 2t(1-t) * P1 + t^2 * P2, t[0,1] –бір қарағанда түсініксіз болып көрінеді. Сондықтан бірден қолдануын қарастырайық.
Екінші дәрежелі Безье сызығын салып шығу үшін үш нүктенің координатасын білу қажет 3 суретті қара.
Бастапқы нүктенің (x0, y0);
аралық нүктенің (x1, y1);
соңғы нүктенің (x2, y2).
t –бастапқы мәні нөль, соңғы мәні бір. Яғни өзгереді 0..1 дейін және мәні өрнектерді есептен сайын артып отырады (мысалы 0,1 –ге). Яғни төменгі өрнектерді 9 рет есептеп қисық сызықтың графигін алуға болады.
x = (1-t) * (1-t) * x0 + 2 * t * (1-t) * x1 + t * t * x2;
y = (1-t) * (1-t) * y0 + 2 * t * (1-t) * y1 + t * t * y2;
Қаламсапты қолға алып Базье сызығын салып шыққан қалды. Декарт жазықтығының бірінші ширегінде жататын үш нүктені таңдаймыз. Мысалға: бастапқы нүктенің x0:=20, y:=20; аралық нүктенің x1:=40, y1:=50; соңғы нүктенің x2:=60, y2:=20 мәндерін тағайындаймыз. Есептеу жүргіземіз. Нәтижесін кестеге толтырамыз. Кестедегі есептеудің нәтижесі бойынша график тұрғызамыз. Графигіміз «доға» тәрізді қисық сызық. Тағы бір рет есептейік. Тек аралық нүктенің координатасын x1:=40, y1:=20 деп аламыз. Басқа нүктенің координаталары өзгеріссіз қалады. Сонда Базье қисығы қандай болады?
Жауабын таптыңыз деп ойлаймын.
Екінші дәрежелі Безье қисық сызығынан басқа үшінші және төртінші дәрежелісі бар.
Компьютерлік графикада үшінші дәрежелі Базье сызықтарды көп қолданысқа ие болды. Corel Draw, Flash, CAD жүйесі Компас 3D программаларында аталған қисық сызық қолданылады. Corel Draw программасында әйгілі «мұрттары»-мен белгілі. Қисық сызықтың мұрттарын жан-жаққа созу арқылы оның пішімі өзгереді.
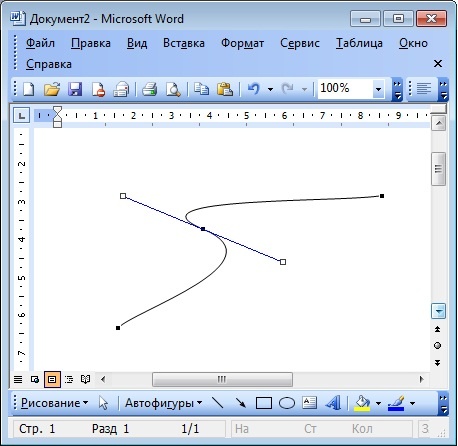
Сурет -4. Осы қисық сызық мұрттарын Word кірістірілген векторлық графикалық редакторынан көруге болады
P.S.: Жазбаға 14/10/2013 16:01 өзгеріс енгізілді.
Жазбаны дайындағанда келесі дерек көздері қолданды:
1) isicad.ru/ru/articles.php?article_num=14924
2) http://ru.wikipedia.org/wiki/Кривая Безье
3) casper.makegames.ru/ispolzovanie-krivoj-beze/

Сурет-1. Citroёn DS
1950 жылдардың басында АҚШ-тың Массачусетс технологиялық институтында CNC -компьютерлік сандық командамен басқарылатын станок ойланып табылды. Келесідей мәселелер өз шешімін күтті:
— детальдің цифрлы моделін алу жолын қарастыру;
— детальдің цифрлық моделі бойынша өңдеп шығаратын станокты басқаратын программаны жасау.
Жоғарыда әңгіме етілген Citroёn DS автомобилінің кузовы «инженерлік мүсін»-ді дәл жасап шығару үшін оны математикалық аппаратпен сипаттауды қажет етті. Автокөлік жасау, аэрокосмос салаларының тапсырыстары бойынша әртүрлі зерттеу топтары үш кеңістегі модельдеу мүмкіншілігін зерттеуге кірісті.
1959 жылы Citroёn автокөлік жасау компаниясына жұмыс істеген француз математигі Поль де Кастельжо «бақылаушы нүктелер» көмегімен геометриялық қасиеттерін сипаттау арқылы «тегіс беттерді» алу жолын ұсынды. Бірақ та ол ашқан сызықтар басқа француз Безье атымен аталады. Поль де Кастельжо жаңалығы «өндірістік құпия болып» сақталынды.
1962 жылдары «Рено» автокөлік компаниясының инженері Безье Пьер көпшілікке өз жаңалығын ұсынды (Поль де Кастельжодан дербес дәл сондай жаңалық жасады). Көп уақыт UNISURF автокөлік кузовтарын жобалайтын компьютерлік бағдарламаны жасаумен шұғылданды. Аталған компьютерлік программаны жасау барысында өнертабыс жасап компьютерлік графиканы дамытуға өз үлесін қосты.
Қазір 3D жобалау арқылы заттың моделін алу заманға ілтипат білдіру болып кетті. Ондай ілтипатты бізде көрсетейік. 3D принтер.

Сурет-2. «3D принтер». Барабандағы пластик шыбықты балқыту арқылы төмендегі мүсінді құйып шықты. Мүсін дәл ортада платформа үстінде тұр («мүйізге» ұқсас).
3D принтер көмегімен алынған мүсін іші қуыс. Қабырғасының қалыңдығы 2 мм. Мүсінді 3D принтер табанынан бастап үстіне дейін бір қабат пластмасса үстіне екінші қабат пластмассаны түзеу арқылы жасап шығарды. Әр қабаттың қалыңдығы мөлшермен 0,3 мм және өзіне тән профилі бар. Профильді түзеу үшін платформа принтердің басының астында қозғалады. Платформаны қозғау үшін екі қозғалтқыш қолданылады. Әр қозғалтқыш платформаны ілгері — кері қозғалысқа келтіреді, яғни х, у бағыттары бойынша.
Енді ең басты. Қалайша қарапайым ілгері – кері қозғалыс арқылы мүсінді құрайтын жаңа қабаттың профилін алуға болатын ойланайық. Көмекке математика келеді. Профиль қисық сызықтар контурынан тұрады. Егер қисық сызықты құрайтын барлық нүктелердің координаталарын білсек онда нүктелерді х, у координатасын анықтап платформа қозғалтқыштарына бере берсек болғаны. Алайда бәрі оңай болса ғой. Профиль контурын анықтайтын графиктің функциясын табу қиын. Пьер Безье қалаған контурын алу үшін функцияны тауып алды. Оның көмегімен координата жазығында оп-оңай конструктор қалаған пішімде кез-келген сызық түсіре алды.
Шын мәнінде 3D принтеріміз CNC станогы ғой!
Базье неге қол жеткізгенін түсіну үшін «Безьенің» екінші дәрежелі қисық сызығын қарастырайық.

Сурет -3. Екінші дәрежелі Безье сызықтары. Бірінші қисық сызық салыну үшін тең бүйірлі үшбұрыштың төбелерінде жататын үш нүкте таңдалынып алынады. Екінші қисық сызық салыну үшін бір түзу бойында, бір-бірінен бірдей қашықтықта жататын үш нүкте алынады.
Екінші дәрежелі Безье сызығының қасиетін бағалау үшін доғаның «алу» жолын көз алдымызға елестетіп көрейік. 3-ші суреттегі ортаңғы нүкте төмен сырғып түскенде «доға» түзуге айналғанын елестету қиын емес. Мұндай қасиеті бар «қисық» сызықты қалай сызуға болады?
Теорияда екінші дәрежелі Безье қисық сызығының теңдеуі келесідей:
B(T) = (1-t)^2 * P0 + 2t(1-t) * P1 + t^2 * P2, t[0,1] –бір қарағанда түсініксіз болып көрінеді. Сондықтан бірден қолдануын қарастырайық.
Екінші дәрежелі Безье сызығын салып шығу үшін үш нүктенің координатасын білу қажет 3 суретті қара.
Бастапқы нүктенің (x0, y0);
аралық нүктенің (x1, y1);
соңғы нүктенің (x2, y2).
t –бастапқы мәні нөль, соңғы мәні бір. Яғни өзгереді 0..1 дейін және мәні өрнектерді есептен сайын артып отырады (мысалы 0,1 –ге). Яғни төменгі өрнектерді 9 рет есептеп қисық сызықтың графигін алуға болады.
x = (1-t) * (1-t) * x0 + 2 * t * (1-t) * x1 + t * t * x2;
y = (1-t) * (1-t) * y0 + 2 * t * (1-t) * y1 + t * t * y2;
Қаламсапты қолға алып Базье сызығын салып шыққан қалды. Декарт жазықтығының бірінші ширегінде жататын үш нүктені таңдаймыз. Мысалға: бастапқы нүктенің x0:=20, y:=20; аралық нүктенің x1:=40, y1:=50; соңғы нүктенің x2:=60, y2:=20 мәндерін тағайындаймыз. Есептеу жүргіземіз. Нәтижесін кестеге толтырамыз. Кестедегі есептеудің нәтижесі бойынша график тұрғызамыз. Графигіміз «доға» тәрізді қисық сызық. Тағы бір рет есептейік. Тек аралық нүктенің координатасын x1:=40, y1:=20 деп аламыз. Басқа нүктенің координаталары өзгеріссіз қалады. Сонда Базье қисығы қандай болады?
Жауабын таптыңыз деп ойлаймын.
Екінші дәрежелі Безье қисық сызығынан басқа үшінші және төртінші дәрежелісі бар.
Компьютерлік графикада үшінші дәрежелі Базье сызықтарды көп қолданысқа ие болды. Corel Draw, Flash, CAD жүйесі Компас 3D программаларында аталған қисық сызық қолданылады. Corel Draw программасында әйгілі «мұрттары»-мен белгілі. Қисық сызықтың мұрттарын жан-жаққа созу арқылы оның пішімі өзгереді.

Сурет -4. Осы қисық сызық мұрттарын Word кірістірілген векторлық графикалық редакторынан көруге болады
P.S.: Жазбаға 14/10/2013 16:01 өзгеріс енгізілді.
Жазбаны дайындағанда келесі дерек көздері қолданды:
1) isicad.ru/ru/articles.php?article_num=14924
2) http://ru.wikipedia.org/wiki/Кривая Безье
3) casper.makegames.ru/ispolzovanie-krivoj-beze/

4 пікір